Обучаем школьников решать открытые задачи

Современные тенденции и методы их внедрения в образовательный процесс российскими исследователями освещались неоднократно. Подчеркнем две из них, которые, на наш взгляд, являются наиболее ярко выраженными.

Во-первых, среди целей, предъявляемых к современному школьному образованию, выделяется формирование личности, способной решать поставленные перед ней задачи в условиях рыночной экономики, в частности, быстро находить наиболее оптимальное и эффективное решение преодолеваемой проблемы. Такая цель направлена на реализацию внутреннего потенциала школьника, развитие творческого начала, его креативности.

Во-вторых, все более остро обозначаются проблемы интеграции в образовании, раскрывающиеся в фундаментальном изучении дисциплин и, в то же время, межпредметных связях с другими образовательными областями. Однако вопросы организации учебно-воспитательного процесса, в котором на основе интегрированного подхода подготавливается выпускник школы, обученный основным практикам жизнедеятельности общества, затрагиваются мало, с позиции его необходимости, а не конкретной реализации.

В данной статье на примере авторского курса «Тренинг креативного мышления» предлагается одна из возможных реализаций обозначенных тенденций, при которых учебно-воспитательный процесс направлен на развитие креативности ученика в интегративной связи математики с другими образовательными областями.

Математика стимулирует развитие логического, образного мышления, конструктивных способностей, позволяет обеспечить достаточно широкий спектр творческой мыслительной деятельности. Это обосновывает выбор данного предмета в качестве педагогического средства.

Целью тренинга является содействие развитию креативной мыслительной деятельности средствами математики. Концепция обучения базируется на использование ТРИЗпедагогики, содержащей, на наш взгляд, наиболее педагогически структурированные приемы и методы активизации мышления человека.

Тренинг разбит на девять взаимосвязанных занятий. В начале каждого занятия ученикам предлагается проблемная ситуация, попытки разрешения которой зачастую приводят к неэффективному решению, в основном изза использования только раннее изученных методов или жизненного опыта. В такой работе происходит актуализация знаний, после чего ученики «подталкиваются» педагогом к наиболее оптимальному и эффективному решению, обобщение которого приводит к новому приему активизации мышления.

Так, например, после изучения на первом занятии метода проб и ошибок, в начале второго занятия предлагаются следующие рассуждения.

Такой метод решения поставленной проблемы, когда перебираются все «попавшие» в поле зрения варианты, мы рассмотрели на прошлом занятии и назвали его методом проб и ошибок. А теперь представьте, что у Светы не 10 платьев, а 100 или даже 1000, или и того больше. Сколько тогда ей понадобится времени, чтобы найди нужное платье. Час, два, неделю, а потом и на дискотеку идти будет поздно. Точно также при решении задач неэффективно перебирать все варианты, на это может уйди очень много времени. Так, например, решая какоелибо уравнение, легче его именно «решать», а не перебирать варианты решений. Поэтому нам нужны какието новые способы, которые более эффективно решают поставленные перед нами задачи. Один из них мы сегодня разберем.

После этого вводится новое понятие — «идеальный конечный результат» (ИКР), использование которого позволяет более эффективно решить проблему девочки — выбор платья для дискотеки, поскольку формируется критерий выбора именно платья для дискотеки с заранее сформулированным предпочтением.

Дальнейший ход занятия направлен на отработку ИКР по двум направлениям: прикладному (жизненных ситуаций) и практическому (математических задач).

Отработку прикладного направления рассмотрим на примере изучения метода обратного мозгового штурма. Учащиеся класса разбиваются на микрогруппы. Перед ними ставится следующая проблема.

Группа, сумевшая найти наименьшее суммарное расстояние, считается победителем. Помимо изучения нового метода, учащиеся получают возможность знакомства с задачами логистики и экономики, решаемыми математическими методами.

Отработку практического направления покажем на примере метода мозгового штурма.

Для решения учащимся предлагается следующая задача.

Коллективное (групповое) решение этой задачи методом мозгового штурма приводит к разнообразным выводам. Наиболее оптимальное и эффективное из них, как правило, попутно подводит к изучению темы «Подобные треугольники».

Рассмотрим два из возможных варианта решения.

Первый вариант предполагает, что человек AB стоит и смотрит на здание ED (рис. 1). Измерив расстояния AD и AO, зная свою высоту AB, можно рассмотреть подобные треугольники BEC и ОВА, из соотношения сторон которых можно узнать искомое.

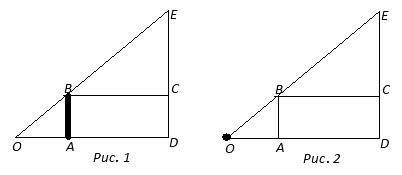
Второй вариант решения предполагает, что человек смотрит из точки О на некоторый предмет AB, высоту которого мы можем измерить, например, палку (рис. 2). Тогда из подобия тех же треугольников, что и в первом варианте с легкостью находится искомое.

После разбора решений задачи деятельность школьников направлена на индивидуальное решение поставленных перед ними проблем, в ходе которого идет отработка введенного приема или метода. В конце занятия, после подведения итогов, ученики получают творческое домашнее задание, при решении которого они знакомятся с новым прием активизации знаний или структурируют иже имеющиеся знания.

При апробации представленного вкратце тренинга как в классах с углубленным изучением математики, так и в общеобразовательных классах, был выявлен рост креативности по параметрам «беглость», «гибкость», «оригинальность», «разработанность» в среднем на 9%. При этом наибольший рост был определен у учащихся общеобразовательных классов, что говорит о привитии интереса к математике при данном обучении.

Таким образом, предлагаемый подход в обучении удачно объединят две обозначенные выше тенденции современного образования, и позволяет избавиться от неоправданного введения двух инновации параллельно друг другу.

¹ Задача взята из личной картотеки А.А. Гина.