Качественное образование: опорные схемы
на уроках математики (тема: "Системы счисления")

Тема «Системы счисления» — одна из основных тем раздела «Основы ЭВМ». В соответствии с государственным стандартом образовательной области «Информатика и ИКТ» тема включает в себя: понятие система счисления, виды систем счисления (позиционная, непозиционная), основания и базис позиционной системы счисления, перевод чисел из одной системы счисления в другую (двоичная, восьмеричная, шестнадцатеричная и десятичная системы), арифметические операции в двоичной системе счисления. Тема «Системы счисления» имеет прямое отношение к математической теории чисел.

В современной информатике используются в основном три системы счисления (все — позиционные): двоичная, шестнадцатеричная и десятичная. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную системы. Являясь смежной с математикой, данная тема вносит вклад также и в фундаментальное математическое образование студентов, но является одной из трудно усваиваемых тем студентами.

Для перевода чисел из одной системы счисления в другую существуют определённые правила. Они различаются в зависимости от формата числа — целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби. Для представления правил перевода чисел из одной систем счисления в другую в более наглядном виде могут быть использованы таблично-матричные логико-смысловые модели, принцип которых был предложен В.Э. Штейнбергом.

Это двумерные структуры, опирающиеся на два признака (основания) изложения материала. Благодаря готовой «сетке», объяснение по такой опоре не занимает много времени и помогает хорошо усвоить материал. Этот тип схем высокоинформативен, даёт возможность установить связи между элементами опоры, имеет чёткое положение каждого элемента в опоре. Таблично-матричная модель удобна тем, что она может быть подана как в готовом (полном) виде, так и заполняться по мере изучения материала. Левая диагональная строка показывает основание системы счисления и число, для которого будет произведён перевод в интересующую систему счисления, расположенную на правой диагональной строке.

Таким образом, в ячейке, расположенной на пересечении диагоналей, установлены связи между правилами перевода целых и дробных чисел. Для нахождения правила для перевода числа из десятичной системы счисления, например, в восьмеричную, необходимо найти число 10 на левой диагонали, в скобках приведено произвольное десятичное число (25)₁₀ и на правой диагонали найти 8, что соответствует основанию нужной для перевода системы счисления. На пересечении диагоналей в ячейке будет приведён пример перевода произвольного числа (25)₁₀. При совпадении оснований систем счисления, на пересечении изображён знак , показывающий, что в этой ячейке правило отсутствует.

Опыт показывает, что диагональные таблично-матричные модели усваиваются лучше, чем обычные прямоугольные. Это давно используют и специалисты в области дизайна графической рекламы: «Диагональ, несомненно, является универсальным организующим принципом в макетировании рекламы»¹.

Примером вертикально-диагональной таблично-матричной модели могут служить разработанные нами модели «Перевод целых чисел из одной системы счисления в другую» и «Перевод дробных чисел из одной системы счисления в другую».

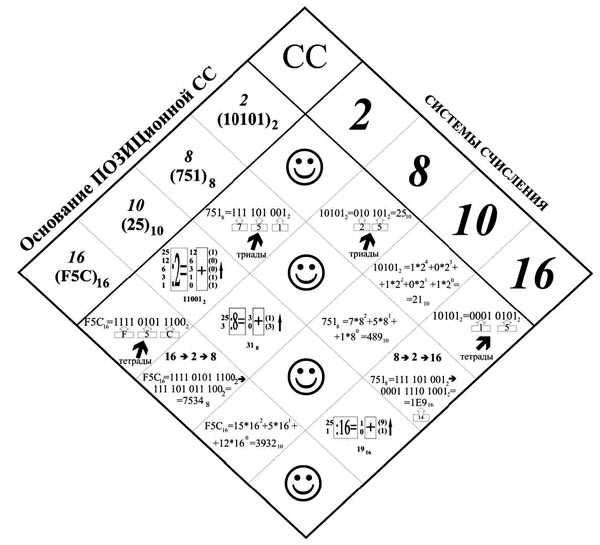
Рис.1. Перевод целых чисел из одной системы счисления в другую

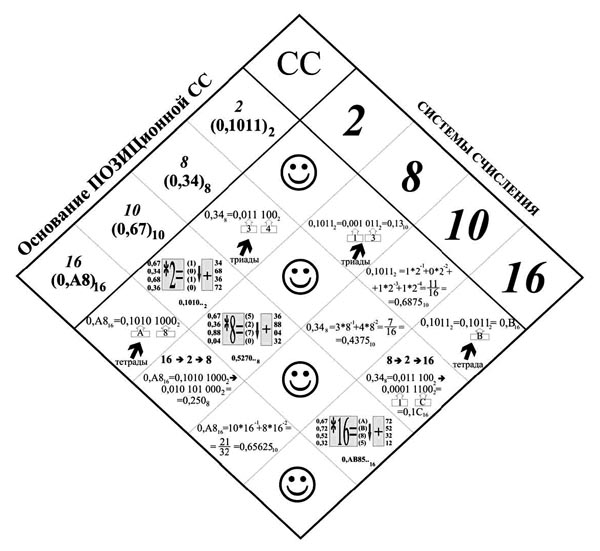
Рис. 2. Перевод дробных чисел из одной системы счисления в другую

Использование рассмотренных опорных схем показало, что они положительно влияют на обучение студентов, особенно тех, которые вначале испытывают трудности при выполнении различных примеров. Схемы могут использоваться только при обучении раздела «Основы ЭВМ», так как для автоматического перевода существует множество программ, позволяющих переводить числа из одной системы счисления в другую. Например, программа «Калькулятор», входящая в стандартный набор ОС Windows.

Исследование выполнено в рамках масштабного педагогического исследования технологии концентрированного обучения, проводимого в рамках деятельности экспериментальной площадки Федерального института развития образования (научный руководитель — д.п.н., проф. А.А. Остапенко).

Перепечатано из журнала «Педагогическая техника» №6-2008.

1 Vestergaard T., Shroder K. The language of Advertising. Oxford, New York. 1985. P.46.