Создание образных моделей для арифметических действий инструментами ТРИЗ

Под ситуацией «Дети плохо считают» чаще всего подразумевается умение производить арифметические действия в уме в пределах сотни.

1-й шаг

Определить, какими путями закладывается это умение: действиями с количественными образами; действиями с числами и цифрами.

Первый путь стал основой программ раннего развития детей в институте им. И.Томаса (США)³. По нему сделана Б.П.Никитиным игра «Точечки»⁴.

Суть данного направления в том, что дети производят умственные математические действия с количеством предметов, а не с обозначающими их числами.

Второй путь основывается на знании таблиц сложения и умножения. Он наиболее распространен в учебных заведениях с классно-урочной системой обучения. Навык отрабатывается выучиванием таблиц и решением большого количества примеров. Такой путь абстрактен и вызывает у многих детей трудности в заучивании таблиц и в выполнении математических действий.

С данной проблемой хорошо знакомы учителя начальных классов, которые очень часто переводят абстрактные действия с числами в действия с предметами типа «яблок», «конфет» и т.п. То есть переходят на первый путь — на действия с количественными образами.

Исходя из вышесказанного, делаем:

2-й шаг Формулируем задачу перехода от первого вида действий ко второму: абстрактные числовые выражения превратить в действия с количественными образами.

Проще говоря, это значит, что абстрактный математический материал должен быть представлен в образной форме. Данная задача решена и решается многими учителями, методистами, учеными, писателями, поэтами, художниками.

3-шаг Минимизировать систему, что означает вывести из процесса перехода от абстракций к количествам учителя. Ученик САМ может превращать абстрактный материал в действия с количественными образами.

При такой постановке задачи, решения принимают вид художественно оформленных рабочих тетрадей для детей.

4-шаг Определим, что должно быть в таких рабочих тетрадях, т.е. их содержание: абстрактный материал в виде числовых выражений; образный материал в количественном выражении.

Работаем по очереди с каждым содержанием.

Шаг 5.1 Абстрактный материал. Описать его части и требования к ним.

• Числовые выражения, например: 8 + 7; 11 — 3. Они задаются извне в готовом виде и записываются, как данность.
• Ответ. Он ищется ребенком и имеет два качества: правильность, неправильность.

Правильность решения выражения, как правило, самим ребенком не определяется. Это делает учитель или ответ примера сверяется с готовым ответом.

Шаг 5.2 Действуем по правилу ИКР (идеального конечного результата). Это правило требует исключить из системы учителя и готовые ответы, а их функции передать ученикам.

Ученик должен САМ узнать правильность или неправильность своего ответа.
Такой формулировке отвечает действие, называемое «ПРОВЕРКА».

Шаг 5.3 Определим, какие бывают проверки для арифметических действий.

• Проверка другим действием. Например, 8 + 7 = 15 проверяется 15 — 8 = 7.
• Проверка счетом. Дети начинают про себя просчитывать число по одной единице в ту или другую сторону.
• Проверка заложена в правильном ответе. Например, при умножении на 9:
  2 х 9 = 18, 3 х 9 = 27, 4 х 9 = 36,... Проверка заключается в том, что сумма цифр ответа равна 9-ти: 1+8, 2+7, 3+6,…

Шаг 5.4 Сформулируем требование к проверке по правилам ТРИЗ.

ОТВЕТ должен сам показывать правильность решения.
Очевидно, что под эту формулировку подходит только 3-й вид проверки.

Шаг 5.5 Ужесточим новой формулировкой требования к ОТВЕТУ.

Сделать неправильный ОТВЕТ невозможно.

Шаг 6.1 Описать требования к образному материалу:

• его можно посчитать,
• его легко и быстро может сделать ученик или иметь в готовом виде.

Шаг 6.2 Выбрать вид образного материала: натуральные и рисованные объекты (яблоки, конфеты, птички и т.п.); пальцы, палочки; простые знаки и фигуры (квадраты, точки, круги, линии и др.).

Выбор делаем по правилу ТРИЗ о «ресурсах», которое гласит:
«Материал должен быть в большом количестве, в готовом виде и легко доступным».

Под эту формулировку подходят следующие образы: квадраты, готовые клеточки в тетради, линии, вертикальные и горизонтальные в клетчатой тетради, точки, на пересечении линий.

Шаг 7 Перейдем к общей формулировке задачи по проблеме: «Арифметические действия с абстрактными числами», согласно шагам 3, 5, 6.

1-й вариант: действия с числами должны превращаться учениками в действия с клеточками, линиями, точками. Полученный ответ должен показывать правильность решения.

2-й вариант: действия с числами должны превращаться учениками в действия с клеточками, линиями, точками, при этом нельзя получить неправильный ответ.

Найдем решение задачи по формулировке 1-го варианта.

Шаг 8.1 Превратить ключевое слово формулировки — «ПРАВИЛЬНОСТЬ» в «ОБЪЕКТ». Описать ее параметры.

Правильность определяется по совпадению результата действия с каким-либо критерием, причем для нашего случая критерий должен находиться в данных решаемого выражения, т.к. мы уже определились, что нельзя пользоваться подсказками ни учителя, ни учебника. Вспомним критерий для умножения чисел на 9. Им является само число 9, получаемое суммированием чисел произведения.

2 х 8 =18 проверка 1+ 8 =9; 3 х 9 = 27 проверка 2 + 7 = 9, 4 х 9 = 36 проверка
3 + 6 = 9 и т.д.

Надо найти или создать жесткую связь ответа с заданными числами.

Математики смогли найти такую связь для произведений числа 9. Мы не будем искать такие закономерности для других чисел, а создадим новые с помощью инструментов ТРИЗ, для решения данной конкретной задачи.

Шаг 8.2 Создание недостающей связи путем перехода к «БИСИСТЕМЕ».

«БИ» — значит «ДВА». В данном случае наша образная математическая модель должна состоять из двух выражений, причем второе выражение должно показывать правильность решения первого.

Такие системы уже существуют и называются ПРОВЕРКОЙ ВТОРЫМ ДЕЙСТВИЕМ (п.1 в шаге 5.3). Их главный недостаток в том, что проверка осуществляется также арифметическим действием. 6 + 4 = 10 проверка 10 — 4 = 6.

Т.е. вид связи остается тем же самым.

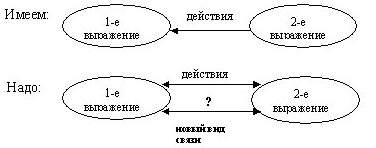
Шаг 8.3 Нахождение нового вида связи.

Вид связи определяется параметрами количественных образов: клеточек, линий, точек и параметрами числового выражения.

Шаг 8.3.1 Определить параметры количественных образов.

Параметры должны иметь конкретные значения.

Для клеточек это: размер, количество, местоположение. Для линий — размер (длина, единица измерения — одна клеточка), количество, направление, местоположение. Для точек — количество, местоположение. (Размер точки конкретно не определим в единицах измерения).

Что выбрать? При этом надо учесть, что один из параметров будет использован для связи арифметическими действиями. Для клеточек действия могут производиться с их количеством или размером. Для линий с количеством и размером. Для точек только с количеством.

Дадим формулировки задач для каждого количественного образа.

• Найти зависимость местоположения клеток от увеличения или уменьшения их количества или размера.
• Найти зависимость местоположения и направления линий от увеличения или уменьшения их длины или количества.
• Найти зависимость местоположения точек от увеличения или уменьшения их количества.

Вероятность найти зависимость легче там, где больше параметров и есть готовый математический инструмент. Выбираем вторую формулировку и обращаемся за помощью к векторной геометрии.

Итак, мы выбрали в качестве образного объекта ЛИНИЮ.

Теперь, чтобы создать новую связь надо определить параметр и его критерий, который будет определять ПРАВИЛЬНОСТЬ решения (см. шаг 8.1).

В нашем распоряжении местоположение и направление.
Критерии местоположения: начало и конец.
Критерии направления: лево, право, верх, низ, наискосок под 45 градусов.

Нагляднее фиксируется совпадения начала и конца, чем совпадение направлений.

Тогда задача для создания новой связи будет звучать так: разработать правила действий с размером и количеством линий, при которых начальное местоположение первого математического выражения совпало бы с конечным местоположением второго выражения.

Чтобы начало совпало с концом, надо менять направление в зависимости от вида арифметического действия или частей абстрактного выражения.

Шаг 8.3.2 Определить параметры абстрактного выражения.

• арифметическое действие или названия частей: слагаемые, уменьшаемое, вычитаемое, сумма, разность, множимое, множитель, произведение, делимое, делитель, частное.
• количество частей;
• конкретные числа.

Например, для выражения 4 + 7 = 11.
Названия: слагаемые и сумма,
Kоличество частей: 3 — два слагаемых и одна сумма,
Числа: 4, 7, 11.

Шаг 8.3.3 Связать параметры ЛИНИЙ с параметрами числового выражения.

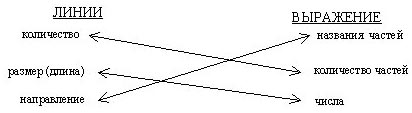
Местоположение у нас выбрано для определения ПРАВИЛЬНОСТИ ответа.

Очевидное решение: заменять количество частей на количество линий, числа на длину линий, а названия частей или действия на направления.

Шаг 8.3.4 Сформулировать задачу для связи двух выражений преобразованных в ЛИНИИ: выбрать начало линий и их направления по названиям 1-го выражения так, чтобы направления и длина линий 2-го выражения привели в исходную точку.

В таком описании задачу можно привести к геометрическому виду и решать с помощью математических инструментов.

Автором была найдена геометрическая модель выражений вида: a + b = c; a — b = c.
Рассмотрим их по отдельности. Модели строятся на тетрадочном листе в клетку.

1. a + b = c
Обозначения согласно шагу 8.3.3.

а — первое слагаемое: длина линии — а клеточек, направление слева направо

b — второе слагаемое: длина линии b клеточек, направление снизу вверх

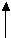
с — сумма: длина линии — с клеточек, направление сверху вниз, слева направо под углом 45 градусов.

Проверочное выражение b + а = c

Для b направление слева направо, а для а снизу вверх.

Сумма с не записывается. Если она была правильно сосчитана в 1-ом выражении, то конец второго слагаемого должен попасть в начало первого выражения.

Если решение не верно, то начало и конец не сойдутся в одной точке.

2. a — b = c
Обозначения согласно шагу 8.3.3.

а — уменьшаемое: длина линии — а клеточек, направление вниз под 450
b — вычитаемое: длина линии — b клеточек, направление слева направо
с — разность: длина линии с клеточек, направление сверху вниз.

Проверочное выражение с + b = а
Для с — направление слева направо, а для b снизу вверх.
Сумма а не записывается.

Если разность 1-го выражения была правильно сосчитана, то конец второго слагаемого должен попасть в начало первого выражения.

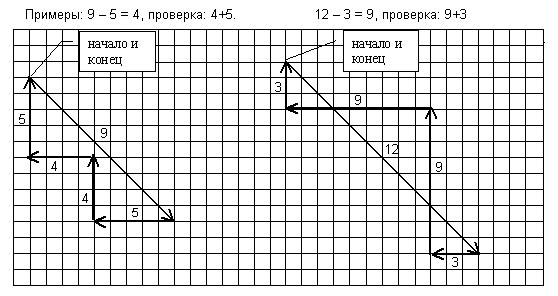
Если решение не верно, то начало уменьшаемого и конец второго слагаемого не сойдутся в одной точке.

Данную линейную модель целесообразно использовать для чисел не более 20-ти, т.к. отрезки становятся очень длинными и неудобными для рисования и счета.

Для больших чисел надо переходить к «ПОЛИСИСТЕМЕ», системе из многих выражений и двух векторному обозначению двухзначных чисел.

Уважаемые коллеги, кто заинтересовался данной моделью и захочет ее использовать в своей работе может обращаться к автору по электронной почте Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.

Литература.

1. Г.С. Альтшуллер, Б.Л. Злотин, А.В. Зусман, В.И. Филатов. Поиск новых идей: от озарения к технологии. Кишинев, 1989.

2. Г. Доман, Д. Доман. Дошкольное обучение ребенка. М.: Аквариум, 1995.

3. Б.П. Никитин. Ступеньки творчества или развивающие игры. М.: Просвещение, 1991.

4. Е.Б. Голицына. Цветные примеры //Карапуз, № 16, 1997.

5. С.В. Ефремов. Таблица умножения Ефремова. Рязань: Пресса, 2000.

Создание образных моделей для арифметических действий инструментами ТРИЗ