Учить по-тризовски, как?

Гомель, 2004

Расположенность к творчеству — высшее проявление активности человека, способность создавать нечто новое, оригинальное в любой сфере человеческой деятельности.

В современных условиях количество изменений в жизни, происходящих за небольшой отрезок времени, настоятельно требуют от человека качеств, позволяющих творчески и продуктивно подходить к любым нововведениям. Для того чтобы выжить в ситуации постоянных перемен, чтобы адекватно на них реагировать, человек должен активизировать свой творческий потенциал.

На протяжении длительного периода обучение в школе ориентировалось на формирование, прежде всего знаний, умений и навыков, носило репродуктивный, информационный характер. В настоящее время происходит переориентация образования на развитие творческих качеств личности.

Среди инновационных технологий обучения детей творчеству ведущее место, на наш взгляд, занимает технология Г.С. Альтшуллера — теория решения изобретательских задач (ТРИЗ).

К числу базисных идей ТРИЗ относятся следующие: теория — катализатор творческого решения проблемы; знания — инструмент творческой работы, творческими способностями наделен каждый (изобретать могут все); творчеству, как и любой деятельности, можно научиться. Особое место в обучении занимает курс Развития Творческого Воображения (РТВ), предназначенный для преодоления стереотипов мышления, выработки умения работать с нетривиальными идеями.

В основе используемых в ТРИЗ-педагогике средств изначально лежит проблемно-поисковый метод, что сближает эту технологию с развивающим обучением.

Общими чертами названных технологий являются:

• сама идея развивающего обучения и развивающего образования;
• деятельностный подход в обучении;
• направленность на формирование теоретических обобщений;
• диалогическая форма общения учителя и ученика;
• использование в обучении проблемных задач;

В то же время между названными технологиями существуют отличия, которые для наглядности представлены таблицей:

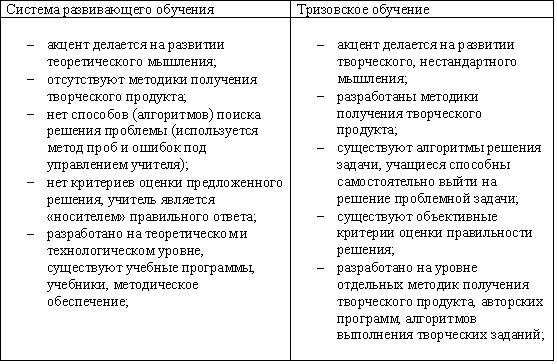
Первоначально ТРИЗ была создана для применения в инженерной деятельности, но те закономерности, на которых она основана, позволяют ее использовать и в других областях, в том числе с 1989 гг. — в педагогике (ведущие разработчики ТРИЗ-педагогики Березина В.Г., Гафитулин М.С., Гин А.А., Злотин Б.Л., Зусман А.В., Кавтрев А.Ф., Камин А.Л., Мурашковская И.Н., Мурашковский Ю.С., Нестеренко А.А., Сидорчук Т.А., Тимохов В.И. и др.)

Многолетний опыт коллег убедительно доказывает возможность применения ТРИЗ в обучении, начиная с дошкольного возраста и младшего школьного возраста.

Представляется необходимым показать сравнительные особенности преподавания с использованием различных методик на конкретном учебном материале. В качестве иллюстрации выбрана тема из курса математики 2 класса «Порядок вычислительных действий».

При традиционной системе обучения учитель объясняет, что «сила» арифметических действий различная. Умножение и деление «сильнее», чем сложение и вычитание. Например, в выражении 2+3·5 число 3 с одной стороны связано знаком «+», а с другой стороны знаком «·». Этот последний знак связывает сильнее, поэтому сначала нужно выполнить умножение, а потом сложение.

Описание методики проблемного обучения дается по книге М.И. Махмутова «Организация проблемного обучения в школе»:

«Учитель записал на доске перед уроком и закрыл два примера: 2+3·5=25 и 2+3·5=17. В этой задаче заложено объективное противоречие между формой и содержанием, между причиной и следствием, между данным и требованием. Это объективное противоречие разрешено в науке путем введения понятия «скобки» (учащиеся еще не знакомы с правилами порядка действий арифметических операций). Противоречие самого понятия «скобки» как противоречие внутренних отношений задачи находится как бы в скрытом виде, внешне проявляясь в противоречии между ее данными и требованием. Именно это внутреннее противоречие объекта должно быть заострено так, чтобы оно воспринималось учащимися как две стороны одного понятия, как логическое противоречие.

После того, как учащиеся прочитали запись примеров, они выражают реакцию удивления. В сознании возникает проблемная ситуация, вызванная противоречием между ранее усвоенными правилами решения и новым фактом, к которому не применимы эти правила.

Последующий анализ проблемной ситуации может идти путем рассуждения о разной последовательности арифметических действий. Ученики объясняют, что в первом случае надо произвести сложение, потом умножение, а во втором — вначале умножение, потом сложение. Для соблюдения именно такого порядка действия необходимо как-то графически обозначить указанную последовательность. Данный теоретический вывод учащихся учитель фиксирует новым понятием «скобки». В этом понятии отражен общий принцип решения задач, аналогичных рассмотренной.»

При обучении с использованием приемов ТРИЗ учитель диктует пример 2+3·5 и предлагает его решить (на доске примеры с разными ответами не записываются, т.к. один из ответов с точки зрения последующего объяснения правила порядка действий является ошибочным).

После проверки ответов выясняется, что при правильном решении получены два разных ответа 17 и 25. Учащиеся догадываются, что неодинаковость ответа вызвана разным порядком вычислительных действий.

Далее предлагается серия примеров на два действия, среди которых есть два одинаковых действия (только сложение (вычитание, умножение, деление)) и смешанные (причем как действия первой ступени, так и двух ступеней). Учащимся необходимо выяснить, всегда ли при наличии двух действий в примере будет два различных ответа.

После анализа результатов данные примеры разбиваются на две группы: имеющие один ответ (то есть порядок действий не влияет на результат) и имеющие два ответа (в которых порядок действий имеет принципиальное значение).

Затем выявляются общие признаки (закономерности) для примеров в каждой группе. Учащиеся приходят к выводу, что примеры в первой группе имеют либо одинаковые знаки действий, либо разные знаки, но относящиеся к одной и то же ступени; а во второй группе оказываются примеры, имеющие действия двух различных ступеней.

Высказывается гипотеза, что разница в ответах будет в том случае, если в примере присутствуют действия разных ступеней. Данная гипотеза проверятся на серии самостоятельно придуманных примеров, и находит свое подтверждение.

И только после этого формулируется проблема: как обеспечить единственность («правильность») ответа в подобных ситуациях? (в процессе обучения у детей уже сформировалось понимание факта, что при одних и тех же исходных данных задачи возможен единственно правильный ответ вне зависимости от способа решения).

Путем анализа различных вариантов дети приходят к двум способам решения примеров «на порядок действий»: нужно или «договориться», какие действия выполняется первыми или каким-то «знаком» обозначить требуемый порядок действий. Учитель сообщает о том, что в примерах, аналогичных данным, нужно вначале выполнять действия умножения/деления либо учитывать скобки (вводится обозначение).

Таким образом, решение проблемной ситуации происходит по алгоритму, характерному для исследований в ТРИЗ:

ТРИЗ — исследование предполагает вторичную обработку информации, причем сама информация зачастую общеизвестна и широко доступна, новизна достигается за счет выбора оснований классификации и новых подходов к обработке фонда. ТРИЗ-подход к обработке информации реализуется через использование ряда моделей, реализующих системный и диалектический взгляд на изучаемый объект.

Большое место в тризовском обучении занимает самостоятельная творческая деятельность учащихся, направленная на получение нового результата. Продуктивная деятельность учащихся младших классов не столько направлена на решение технических учебных задач, сколько на решение и изобретение того, что реальнее и ближе к ним: изобрести загадку, высказать оригинальную гипотезу, сочинить сказку, метафору, пословицу, «да-нетку»; изобрести подвижную игру, придумать новое свойство объекта и его практическое применение, предложить вариант устранения возникшей проблемы в классе, придумать и изготовить новую игрушку и т.д.

Использование в школе методики ТРИЗ организует мышление, делает его системным, учит находить и разрешать противоречия. На этой основе достигается более глубокое усвоение фактических знаний, а главное — формируется стиль мышления, направленный не на приобретение готовых знаний, а на их самостоятельную генерацию; умение видеть, ставить и решать проблемные задачи в своей области деятельности; умение снимать закономерности, воспитание мировоззренческой установки восприятия жизни как динамического пространства открытых задач — что и требуется сегодня в школе для подготовки к завтрашней жизни.