Математическая ниткопись

Ниткопись на уроке математики

Задания. Попробуйте изобразить ниткой на бархатной бумаге прямую линию, треугольник, букву "x", знак квадратного корня.

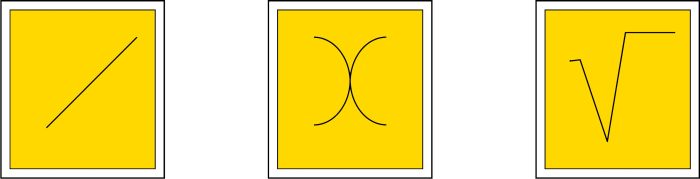
Для того, чтобы ниточка не сдвигалась во время работы, ее надо прижать пальцем за законченным участком изображения и затем уже формировать новый участок.

Для лучшего восприятия изображения нить должна быть контрастной по цвету к фону бумаги. Можно использовать нитки разных цветов, разной длины и количества. Сочетание различных характеристик нитей станет источником творческого замысла как для педагога, так и для ученика.

Несколько примеров заданий по использованию ниткописи в математике:

• Изобразить цифру, с которой начинается номер вашей школы (класса, номера дома или квартиры).
• Изобразить нитками индекс вашего города (форма цифр как на почтовом конверте). Например, один из почтовых индексов г. Жуковского – 140185.
  
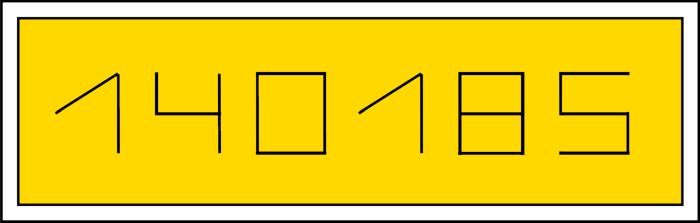
• Используя ниткопись, изобразить числа, которые при сложении между собой не переходят через десяток. У кого больше получится чисел.
• Изобразить нитками ответ к примеру (задаче).

Графики

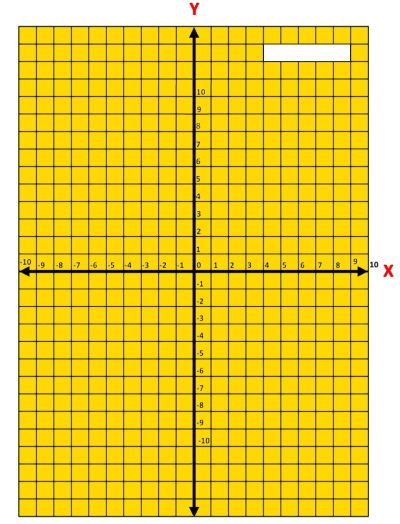
Прямоугольная система координат, нанесенная на светлую бархатную бумагу, - хорошее дидактическое пособие для учителей при изучении различных графиков. Наличие у школьника такого пособия дает возможность педагогу оперативно провести проверку его знаний по умению строить график, выкладываемый ниткой.

На небольшой прямоугольной пластмассовой пластинке, приклеенной в углу пособия, записывается карандашом задание, например уравнение, которое необходимо проиллюстрировать графически.

После выполнения задания запись на пластинке удаляется ластиком. Ученики могут обменяться своими работами и теперь для них возникает обратная задача: по графику составить уравнение.

В случае ошибки ученика при решении задачи график легко исправляется корректировкой положения нити на координатной плоскости.

Это пособие многократного пользования. Длительная работа с одним и тем же листом бархатной бумаги уплотняет ее верхний слой. Восстановить ворсистость можно "почистив" бумагу сухой зубной щеткой.

Перечисленные варианты использования ниткописи не исчерпывают все ее возможности применения на уроках математики.

Делаем пособие «Математическая ниткопись»

С целью повышения интереса учащихся к изучению математики и качества полученных ими знаний было решено использовать идею «ниткописи» при изучении темы «Функции и их графики».

Каждым учеником было изготовлено дидактическое пособие, получившее название «Математическая ниткопись».

Пособие «математическая ниткопись» представляет собой лист-папку.

Лист-папка — это лист ватмана формата А3, сложенный пополам. В сложенном состоянии пособие соответствует формату А4 (формат машинописного листа).

На внутреннем развороте пособия:

1. Слева приклеен почтовый конверт, в котором находятся:

• тонкие ворсистые разноцветные цветные нитки,
• картонные шаблоны различных графиков функций: y = ½x², y = x², y = 2x², y = 3x² и другие

2. Справа приклеен лист светлой бархатной бумаги. На нем нанесена прямоугольная система координат (клетка 1х1 см.). В верхней части разлинованного листа приклеена небольшая прямоугольная пластмассовая пластина. На пластине карандашом записывается задание, которое необходимо проиллюстрировать графически при помощи ниток. После выполнения задания запись на пластине удаляется ластиком. Ученики могут обменяться своими работами и теперь для них возникает обратная задача: по графику функции составить уравнение.

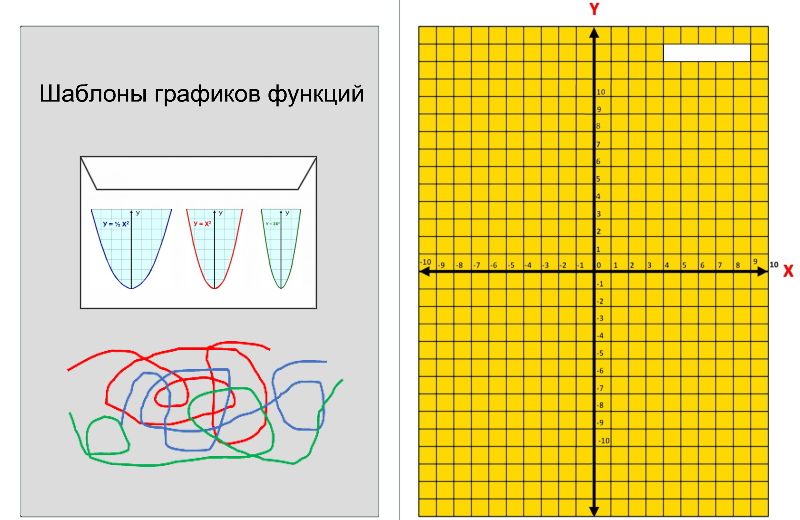
В пособии «Математическая ниткопись» выполнялись следующие типы и виды упражнений по построению графиков функций:

Линейная функция

Примеры упражнений:

а)
y = x
y = x + 2
y = x - 3

б)
y = -3x
y = -3x - 2
y = -3x + 4

в)
Изобразить три параллельных прямых и передать соседу по парте для определения функции.

Выполняя эти упражнения, ученики:

• изображают графически функцию, заданную аналитически;
• закрепляют в памяти смысл коэффициентов k и b в записи линейной функции y = kx + b;
• определяют вид функции, если известен график (прямая и обратная задачи).

Здесь же педагог показывает простейшее преобразование графика функции y = f(x) Þ y = f(x) + b;

Квадратичная функция

При выполнении упражнений данного раздела применяются шаблоны, по контуру которых укладывается нить.

Примеры упражнений:

а)
y = x²
y = x² + 3
y = x² - 4

б)
y = -½ x²
y = -½ x² - 3
y = -½ x² + 4

в)
С помощью любого шаблона изобразить параболу с вершиной на оси ОУ. Передать соседу для определения и записи вида функции.

Примеры упражнений:

а)
y = 2x²
y = -2x²

б)
y = 3x² + 1
y = -3x² + 1

Данные упражнения:

• закрепляют знания о направлении и степени расхождения ветвей параболы;
• иллюстрируют преобразование графика функции f(x) Þ f(x) + b;
• иллюстрируют преобразование графика функции f(x) Þ - f(x)

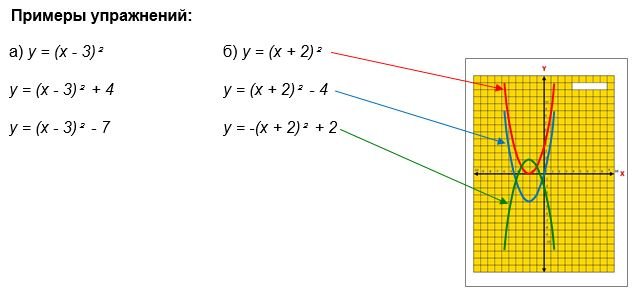
 Данные упражнения:

• иллюстрируют построение параболы с помощью выделения полного квадрата и требуют применения следующих правил преобразования графиков функций: f(x) Þ f(x) + a; f(x) Þ f(x - a);

Примеры упражнений:

а)
y = (x - 3) (x + 1)
y = (x + 2) (x - 1)

б)
y = (2x + 2) (x - 1)
y = (3x - 3) (x + 1)

Данные упражнения:

• юстрируют построение квадратичной параболы по нулям функции и коэффициенту при x² с помощью шаблона.

Данные упражнения:

• иллюстрируют применение преобразование графика функции: f(x) Þ /f(x)/

Функция √¯x,  ³√¯x

Примеры упражнений:

а)
y = √¯x¯´
y = √¯x¯-¯2¯´
y = √¯x¯+¯3¯´

б)
y = ³√¯x¯´
y = ³√¯x¯´ + 4
y = ³√¯x¯´ - 2

в)
y = √¯x²¯´
y = √¯x²¯´ + 1
y = √¯x²¯´ - 7

г)
y = √¯/x/¯´
y = √¯/x¯-¯2/¯´
y = √¯/x¯+¯3/¯´

Выполнение данного упражнения требует от ученика понимания и правильного применения свойств функций y = √¯x¯´ и y = ³√¯x¯´, их сходств и различий.

Графики каждой серии строятся в одних осях координат, что позволяет повторить и закрепить правила преобразования графиков функции, свойство √¯x²¯´ = /x/, нахождение области определения функции.

Кубическая парабола

Примеры упражнений:

а)
y = x³
y = x³ - 2
y = x³ + 7

б)
y = (x - 1)³
y = (x + 2)³ - 3
y = (x - 3)³ + 4 

Результаты и выводы

Приведенные выше и подобные им упражнения были использованы на уроках в 9-ом классе гимназии №1 г. Жуковского.
По результатам нескольких уроков с применением «математической ниткописи», можно сделать главный вывод: идея использования ниткописи на уроках математики интересна и для учеников, и для учителя, а ее использование дает следующие результаты:

1. Урок становится более разнообразным, интересным.
2. Мыслительный процесс соединяется с физическим действием по укладыванию нити, возрастает наглядность.
3. Построение графиков сериями позволяет проиллюстрировать правила построения и преобразования графиков.
4. Решается прямая и обратная задача: построение графика данной функции и нахождение вида функции по данному графику.
5. Эта деятельность способствует более глубокому усвоению материала и повышению самоконтроля учеников.
6. Ученик привыкает строить графики, исходя из набора элементарных функций, преобразуя их, а не вычисляя в таблице большое количество точек.

Практика подсказала, что пособие «математическая ниткопись» желательно применять на уроках математики уже в начальной школе, а затем продолжить работу в среднем звене. Так в 7-9 классах пособие будет полезно при изучении следующих тем:

1. Функции и их графики
2. Решение линейных систем уравнений
3. Графический способ решения уравнений
4. Решение систем уравнений второй степени

Авторы будут рады, если Вас заинтересовала ниткопись, ее «математические» свойства. Надеемся, что Вы решили попробовать свои возможности и возможности учащихся. Желаем творческих успехов в освоении ниткописи.

Литература:

1. Гафитулин М.С. Ниткопись: Творческая изобразительная деятельность //Начальная школа. - 1993- N1.- С.68-69.
2. Галицкий М.Л. и др. Сборник задач по алгебре для 8-9 классов: Учеб. пособие для учащихся шк. и классов с углубл. изуч. курса математики/ М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич. - М.: Просвещение, 1992. С.87-101.